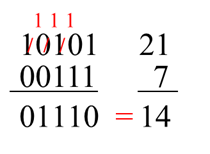Arithmetic Operations and Circuits

Binary Arithmetic

Addition

• There are four basic rules to adding two binary digits.

0 + 0 = 0 carry 0

0 + 1 = 1 carry 0

1 + 0 = 1 carry 0

1 + 1 = 0 carry 1

• Binary digits are added two at a time and any carry must be carried over to the next higher column of digits.
• To get the sum of three digits, add the first two and then add the sum to the third digit.
• To add large binary numbers add one column of digits starting with the least significant position. Add any carry into the next significant column.

For Example:

Add the binary numbers 00111 and 10101 and show the equivalent decimal addition.

Subtraction

• There are four possible combinations when subtracting two binary digits.

0 – 0 = 0 borrow 0

0 – 1 = 1 borrow 1

1 – 0 = 1 borrow 0

1 – 1 = 0 borrow 0

• The borrow from a column of digits must be subtracted from the next most significant column.
• To subtract a large binary number from another large binary number, a borrow may need to be carried over several bit positions.

For Example:

Subtract the binary number 00111 from 10101 and show the equivalent decimal subtraction.

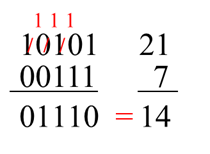
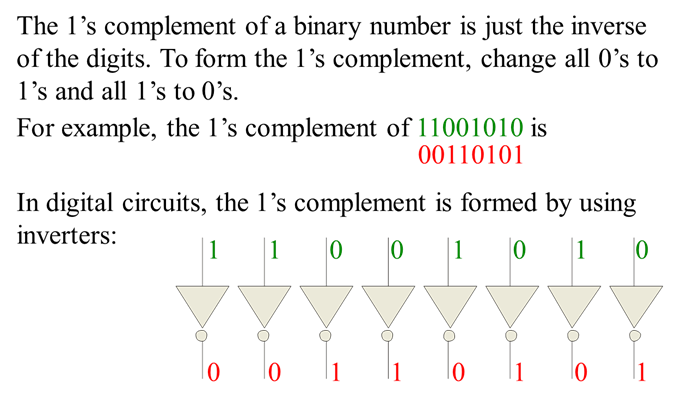
One's Complement Representation

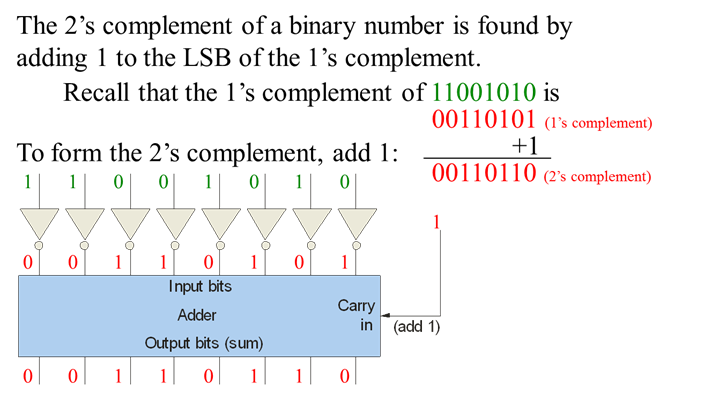
Two's-Complement Representation

• The two's-complement method is one of the most popular methods of representing binary numbers in digital circuits.
• Most computers use an 8-bit or a 16-bit binary word.
• The MSB is the sign bit and a 0 means positive and a 1 means negative.
• Positive numbers are in true form and negative numbers are in two's-complement form.
• the range of positive numbers is 0 to (2^N–1 – 1) where N is the number of bits. (0 to 127 for 8-bit numbers)
• The range of negative numbers is –1 to 2^{N – 1} (–1 to –128 for 8-bit numbers)

Two's-Complement Arithmetic

• In order to add signed numbers, simply perform the standard addition. If the numbers are correctly signed, the answer will come out with the correct sign.
• In order to subtract signed numbers, take the two's-complement of the number being subtracted and add the two numbers.
• When adding and subtracting be sure the answer does not exceed the range of the signed numbers.
  (+127 to –128 for 8-bit numbers; +32,767 to –32,768 for 16-bit numbers)

Hexadecimal Arithmetic

• Hexadecimal is a base 16 number system.
• To add hexadecimal numbers:
1. Add the two hex digits by working with their decimal equivalents.
2. If the decimal sum is less than 16 write down the hex equivalent.
3. If the decimal sum is 16 or more, subtract 16, write down the hex result and carry 1 to the next-more-significant column.
• Hexadecimal addition can also be accomplished by converting the hexadecimal numbers to binary and adding the binary numbers.
• Subtraction of hexadecimal numbers:
1. Subtract the decimal equivalents of the hex digits.
2. If a borrow is needed, subtract 1 from the more-significant digit and add a decimal 16 to the digit being borrowed to.
3. Write down the hex equivalent of the decimal difference.
• Hexadecimal subtraction can be accomplished by converting the hexadecimal number to binary and then performing binary subtraction.

BCD Arithmetic

• BCD is a binary code of the ten decimal digits. It is not a binary equivalent.
• To perform BCD addition
1. Add the BCD digits as regular binary numbers.
2. If the sum is 9 or less and no carry was generated, it is a valid BCD digit.
3. If the sum produces a carry, the sum is invalid and the number 6 (0110) must be added to the digit.
4. If the sum is greater than nine, the sum is invalid and the number 6 (0110) must be added to the digit.
5. Repeat for each of the BCD digits.

Arithmetic Circuits

• The basic process of adding two binary digits can be accomplished with a half-adder circuit.
• In a half-adder, the sum output is the Exclusive-OR of the two input bits. The carry output is the logical AND of the two input bits.

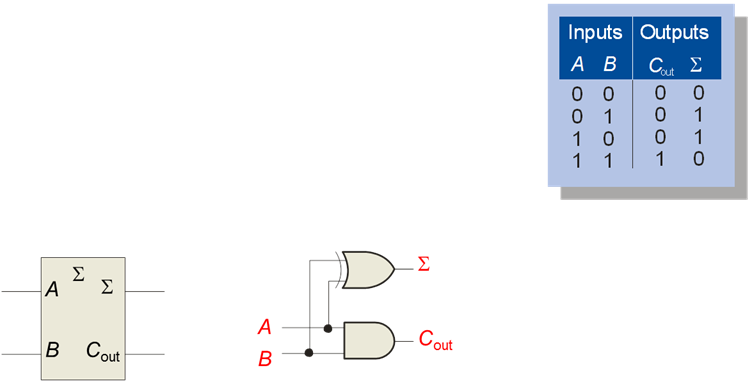
• If a third input is required (carry in from previous-significant digit) then a full-adder circuit must be used.
• A full-adder is really two half-adders with the carry outputs ORed together.

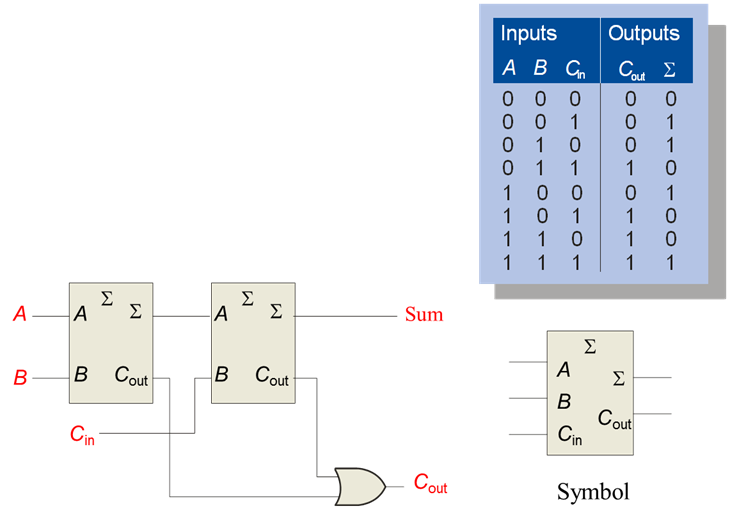
• The full-adder and the half-adder can be represented with a block symbol. The half-adder has two inputs and the full-adder has three inputs.
• In order to add two binary words with several bits, an adder circuit is required for each bit of the date word. to make the circuit complete, the carry input for each full-adder is connected to the carry output of the previous least-significant bit.

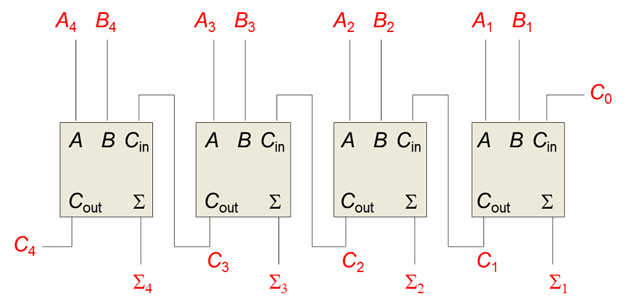
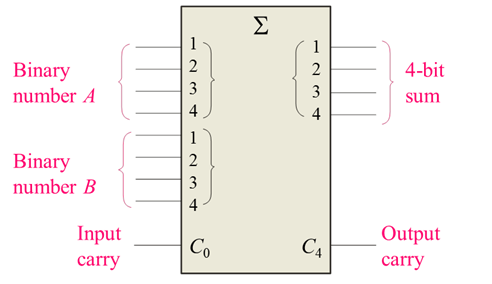
Four-Bit Full-Adder ICS

• There are a number of ICs available that contain adder circuits.
• The 7483 and 4008 are examples of ICs with 4 full-adder circuits.
• The 7483 and 4008 use a fast-look-ahead carry circuit to speed up the circuit propagation time. Without this circuit the carry would have to ripple through all 4 bits.

System Design Applications

• Exclusive-OR gates can be used to perform a controlled inversion of a data word.
• The controlled inversion combined with an additional 1 on the carry input of the LSB of a set of full-adders will give the two's-complement of a number.
• Subtraction can be accomplished by taking the two's-complement of a number and adding.
• BCD addition can be accomplished also with full-adders.
  One set of adder circuits is used to do the original addition. Some addition logic is necessary to detect a carry or an illegal number. A second set of adder circuits is then used to add six to the first sum.
• The 74HC583 is a single chip that will perform all the necessary steps in order to add 2 BCD digits.

Arithmetic/Logic Units

• An ALU can perform several different arithmetic or logical operations.
• The 74181 is a 4 bit ALU with 16 logic and 16 arithmetic functions.

Additional Notes

Signed numbers can be represented with the two's-complement form. In this form the most significant bit is the sign bit. With one bit used as a sign then the magnitude of the number is reduced by one bit. for a data word with 8-bits, the normal capacity would be 256 numbers. With the sign bit there are 128 positive numbers (0 to +127) and 128 negative numbers (–1 to –128). This is still 256 numerical combinations.

Care must be taken, however, when working with signed numbers not to exceed the range of positive or negative numbers. For example: if the number +2 (0000 0010) is added to +126 (0111 1110) the results will be 1000 0000.

This is not +128 but a negative number –127. Two positive numbers added together resulted in a negative answer. This is a condition called overflow. Most computers have special circuits to detect an overflow condition.