Numbering Systems

Decimal Numbers

Decimal is a Base 10 numbering system.

The position of each digit in a weighted number system is assigned a weight based on the base or radix of the system. The radix of decimal numbers is ten, because only ten symbols (0 through 9) are used to represent any number.

The column weights of decimal numbers are powers of ten that increase from right to left beginning with 10⁰ =1: …10⁵ 10⁴ 10³ 10² 10¹ 10⁰.

For fractional decimal numbers, the column weights are negative powers of ten that decrease from left to right: 10² 10¹ 10⁰. 10^-1 10^-2 10^-3 10^-4 …

Decimal numbers can be expressed as the sum of the products of each digit times the column value for that digit. Thus, the number 9240 can be expressed as

 (9 * 10³) + (2 * 10²) + (4 * 10¹) + (0 * 10⁰)

Or

 9 * 1,000 + 2 * 100 + 4 * 10 + 0 * 1

For example: The number 480.52 Expressed as the sum of values of each digit is.

480.52 = (4 x 10²) + (8 x 10¹) + (0 x 10⁰) + (5 x 10^-1) + (2 x 10^-2)

Or

4 * 100 + 8 * 10 + 0 * 1 + 5 * .1 + 2 * .01

Binary Numbers

Binary is a Base 2 numbering system.

For digital systems, the binary number system is used. Binary uses the digits 0 and 1 to represent quantities. 

Each binary position contains one binary digit or bit. The leftmost bit position is called the most significant bit (MSB). The right most bit position is called the least significant bit (LSB).

The column weights of binary numbers are powers of two that increase from right to left beginning with 2⁰ =1:

…2⁵ 2⁴ 2³ 2² 2¹ 2⁰.

For fractional binary numbers, the column weights are negative powers of two that decrease from left to right: 2² 2¹ 2⁰. 2^-1 2^-2 2^-3 2^-4 …

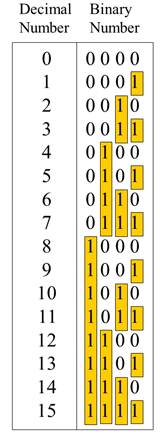
A binary counting sequence for numbers from zero to fifteen is shown.

Notice the pattern of zeros and ones in each column.

Digital counters frequently have this same pattern of digits:

Binary Conversions

The decimal equivalent of a binary number can be determined by adding the column values of all of the bits that are 1 and discarding all of the bits that are 0.

For example: Convert the binary number 100101.01 to decimal.

Start by writing the column weights; then add the weights that correspond to each 1 in the number.

Binary Conversions (cont.)

You can convert a decimal whole number to binary by reversing the procedure. Write the decimal weight of each column and place 1's in the columns that sum to the decimal number. This is called the Sum-of-Weights Method.

For example: Convert the decimal number 49 to binary.

The column weights double in each position to the right. Write down column weights until the last number is larger than the one you want to convert.

32+16+1=49

Binary Conversions (cont.)

You can convert a decimal fraction to binary by repeatedly multiplying the fractional results of successive multiplications by 2. The carries form the binary number.

For example: Convert the decimal fraction 0.188 to binary by repeatedly multiplying the fractional results by 2.

Binary Conversions (cont.)

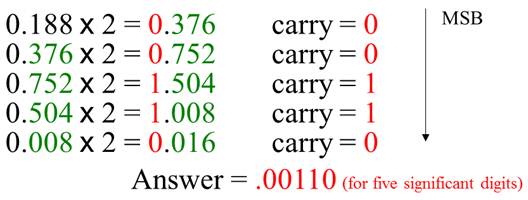
You can convert decimal to any other base by repeatedly dividing by the base. For binary, repeatedly divide by 2. This is called the Successive Division Method.

Repeatedly divide the number by the base 2.

The remainders from each division represent the binary number.

The first division produces the MSB and the last division produces the LSB.

For example: Convert the decimal number 49 to binary by repeatedly dividing by 2.

Place the remainders and 49₁₀ in decimal equals 110001₂ in Binary. 

Hexadecimal Numbers

 Hexadecimal uses sixteen characters to represent numbers: the numbers 0 through 9 and the alphabetic characters A through F.

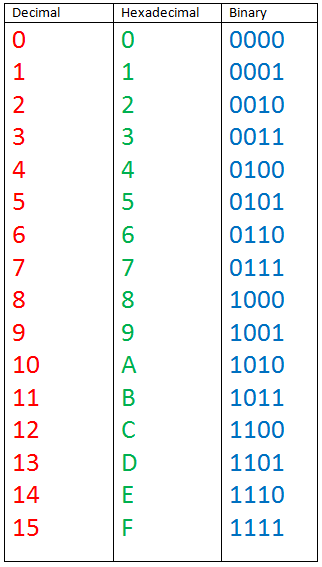
Large binary number can easily be converted to hexadecimal by grouping bits 4 at a time and writing the equivalent hexadecimal character. 

For example: Express 1001 0110 0000 1110₂ in hexadecimal:

Group the binary number by 4-bits starting from the right.

Thus,    

1001       0110       0000       1110 = 960E

9              6              0              E

Hexadecimal Numbers (cont.)

Hexadecimal to Decimal

Hexadecimal is a weighted number system.  The column weights are powers of 16, which increase from right to left.

To express 1A2F₁₆ in decimal you would place the Hexadecimal number in the chart and multiply then add.

Hexadecimal Numbers (cont.)

Decimal to Hexadecimal

Successively divide the decimal number by 16.

The remainders are the hexadecimal digits starting with the most significant digit first.

If the remainder is 10 or greater it must be converted to its hexadecimal letter symbol (A, B, C, D, E, F).

(Note: To find the remainder multiply the decimal portion times the base you are converting to. Only take the whole number down to the next line.)

Lets convert 425₁₀

So 425₁₀ = 1A9₁₆

Hexadecimal Numbers (cont.)

Binary to Hexadecimal

Group the binary bits in groups of four starting with the least significant bit.

Write down the hexadecimal digit that represents each binary group of four.

For example lests convert 110110011011₂

Break into groups of four starting on the right the convert each 4 bit number to the Hexadecimal equivalent.

So 110110011011₂ = D9B₁₆

Hexadecimal to Binary

Write the binary group of four bits that represents each hexadecimal digit.

Lets convert CAB₁₆

So CAB₁₆ = 1100 1010 1011₂

Octal Numbers

Octal uses eight characters the numbers 0 through 7 to represent numbers. There is no 8 or 9 character in octal.

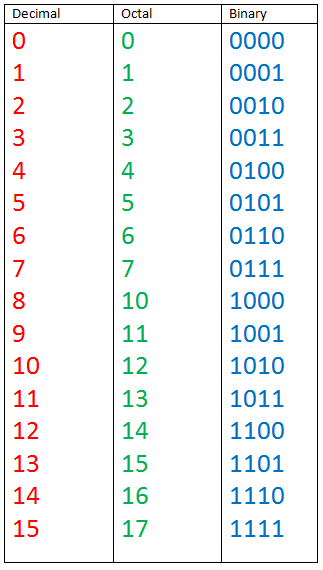
Octal is also a weighted number system.  The column weights are powers of 8, which increase from right to left.

Octal to Decimal

To express 3702₈ in decimal you would place the Octal number in the chart and multiply then add.

Octal Numbers (cont.)

Decimal to Octal

Successively divide the decimal number by 8.

The remainders are the octal digits starting with the most significant digit first.

(Note: To find the remainder multiply the decimal portion times the base you are converting to. Only take the whole number down to the next line.)

Lets convert 629₁₀

So 629₁₀ = 1165₈

Octal Numbers (cont.)

Binary to Octal

Group the binary digits in groups of three starting with the least significant bit.

Write down the octal digit that represents each group of three binary digits.

For example: Express 1 001 011 000 001 110₂ in octal:

Group the binary number by 3-bits starting from the right (Red zeros were added to make the binary number have 3 bits).

Thus,    

001         001         011         000         001         110₂ = 113016

1              1              3              0              1              6₈

Octal to Binary

Write down the binary group of three bits for each octal digit.

Lets convert 175₈

So 175₈ = 001 111 101₂

BCD

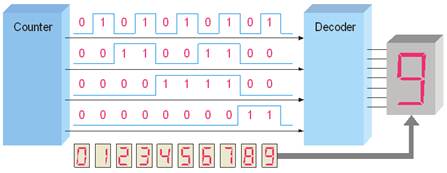
Binary coded decimal (BCD) is a weighted code that is commonly used in digital systems when it is necessary to show decimal numbers such as in clock displays.

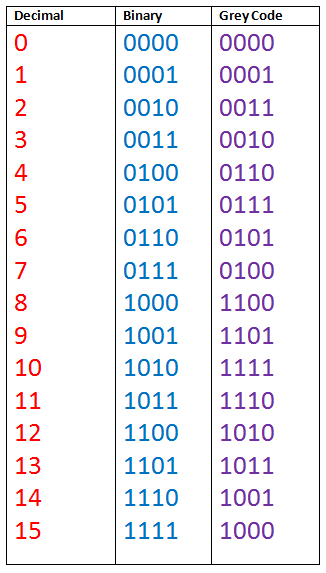
Converting from decimal to BCD and back is the same as converting Hexadecimal. Each digit represents 4 bits of BCD information.

The table illustrates the difference between straight binary and BCD. BCD represents each decimal digit with a 4-bit code. Notice that the codes 1010 through 1111 are not used in BCD.

Gray code

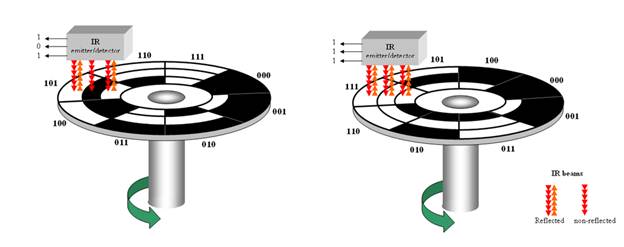
Gray code is an unweighted code that has a single bit change between one code word and the next in a sequence. Gray code is used to avoid problems in systems where an error can occur if more than one bit changes at a time.

Gray code (cont.)

A shaft encoder is a typical application. Three IR emitter/detectors are used to encode the position of the shaft. The encoder on the left uses binary and can have three bits change together, creating a potential error. The encoder on the right uses gray code and only 1-bit changes, eliminating potential errors.

ASCII

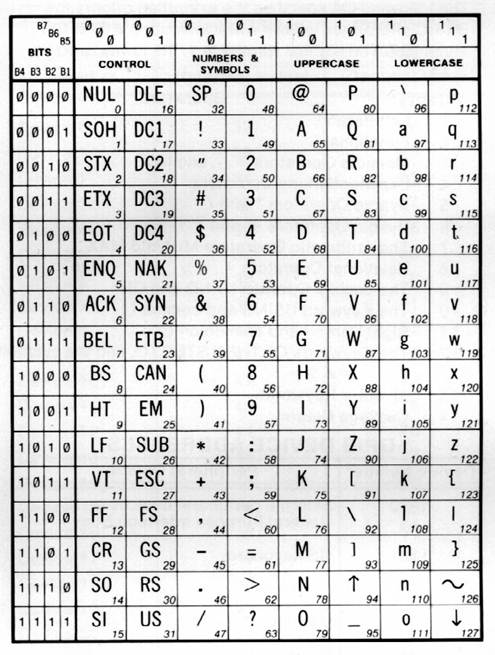
American Standard Code for Information Interchange (ASCII) pronounced "askee".

ASCII is a code for alphanumeric characters and control characters. In its original form, ASCII encoded 128 characters and symbols using 7-bits. The first 32 characters are control characters, that are based on obsolete teletype requirements, so these characters are generally assigned to other functions in modern usage.

The code is divided into a group of 3 bits (MSD) and a group of 4 bits (LSD). For more information Click Here.

In 1981, IBM introduced extended ASCII, which is an 8-bit code and increased the character set to 256. Other extended sets (such as Unicode) have been introduced to handle characters in languages other than English.

Binary Practice

Convert the following numbers. Do not use a calculator.

Hexadecimal Practice

Convert the following numbers. Do not use a calculator.

Octal Practice

Convert the following numbers. Do not use a calculator.