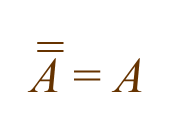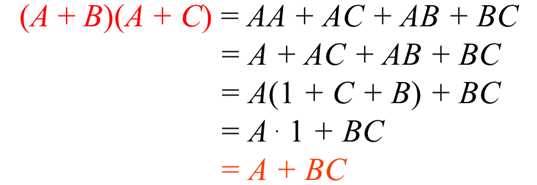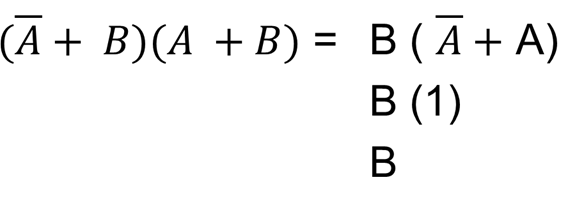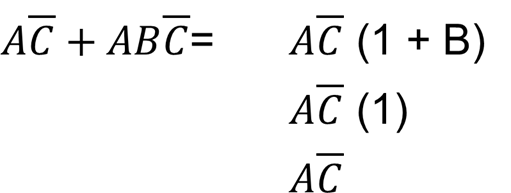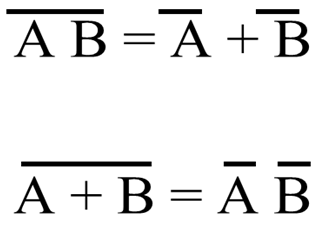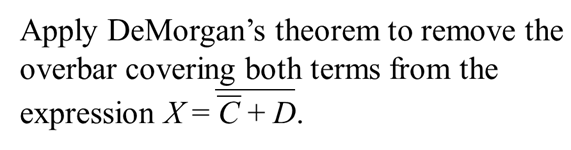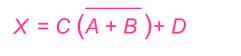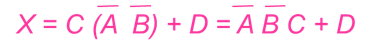Boolean Algebra and Reduction Techniques

Boolean Algebra Laws and Rules

There are three laws of Boolean Algebra that are the same as ordinary algebra.

1. The Commutative Law
   addition A + B = B + A (In terms of the result, the order in which variables are ORed makes no difference.)
   multiplication AB = BA (In terms of the result, the order in which variables are ANDed makes no difference.)
2. The Associative Law
   addition A + (B + C) = (A + B) + C (When ORing more than two variables, the result is the same regardless of the grouping of the variables.)
   multiplication A(BC) = (AB)C (When ANDing more than two variables, the result is the same regardless of the grouping of the variables.)
3. The Distributive Law - The distributive law is the factoring law. A common variable can be factored from an expression just as in ordinary algebra.
   A(B + C) = AB + AC

 (A + B)(C + D) = AC + AD + BC + BD Remeber FOIL(First, Outer, Inner, Last)?

Ten Basic Rules of Boolean Algebra

1. Anything ANDed with a 0 is equal to 0. A * 0 = 0
2. Anything ANDed with a 1 is equal to itself. A * 1 = A
   
3. Anything ORed with a 0 is equal to itself. A + 0 = A
   
4. Anything ORed with a 1 is equal to 1. A + 1 = 1
   
5. Anything ANDed with itself is equal to itself. A * A = A
   
6. Anything ORed with itself is equal to itself. A + A = A
   
7. Anything ANDed with its own complement equals 0.
   
8. Anything ORed with its own complement equals 1.
   
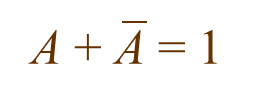
9. Anything complemented twice is equal to the original.
   
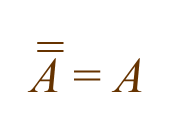
10. The two variable rule.

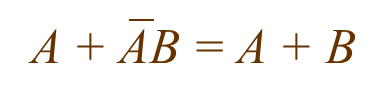
Simplification of Combinational Logic Circuits Using Boolean Algebra

• Complex combinational logic circuits must be reduced without changing the function of the circuit.
• Reduction of a logic circuit means the same logic function with fewer gates and/or inputs.
• The first step to reducing a logic circuit is to write the Boolean Equation for the logic function.
• The next step is to apply as many rules and laws as possible in order to decrease the number of terms and variables in the expression.
• To apply the rules of Boolean Algebra it is often helpful to first remove any parentheses or brackets.
• After removal of the parentheses, common terms or factors may be removed leaving terms that can be reduced by the rules of Boolean Algebra.
• The final step is to draw the logic diagram for the reduced Boolean Expression.

Some Examples of Simplification

Perform FOIL (Firt - Outer - Inner - Last)

AA = A (Anything ANDed with itself is itself)

Find a like term (A) and pull it out. (There is an A in A, AC, and AB). Make sure you leave the BC alone at the end.

Anything ORed with a 1 is a 1 (1+C+B=1).

Anthing ANDed with a 1 is itself (A1=A)

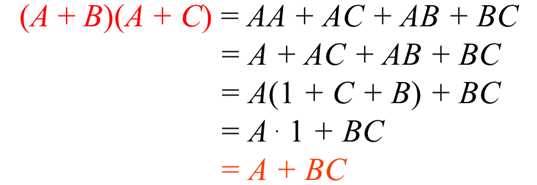
Some Examples of Simplification (cont.)

Find like term (B) and pull it out.

Anything ORed with its own complement equals 1.

Anything ANDed with 1 is itself.

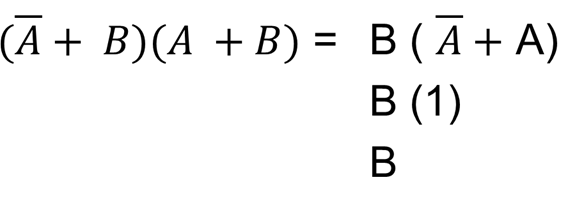
Some Examples of Simplification (cont.)

Find like term and pull them out. Make sure you leave the one.

Anything ORed with a 1 is 1.

Anything ANDed with a 1 is itself

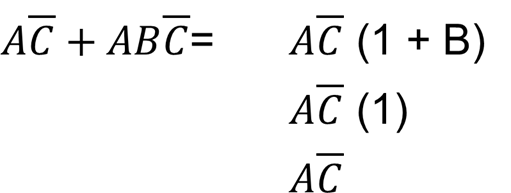
Some Examples of Simplification (cont.)

Find like terms and pull them out.

Anything ORed with its own complement equals 1.

Anything ANDed with 1 equals itself.

NOTE: I will workout many examples in the video.

DeMorgan's Theorem

• De Morgan's theorem allows large bars in a Boolean Expression to be broken up into smaller bars over individual variables.
• De Morgan's theorem says that a large bar over several variables can be broken between the variables if the sign between the variables is changed.
  
• De Morgan's theorem can be used to prove that a NAND gate is equal to an OR gate with inverted inputs.
• De Morgan's theorem can be used to prove that a NOR gate is equal to an AND gate with inverted inputs.
• In order to reduce expressions with large bars, the bars must first be broken up. This means that in some cases, the first step in reducing an expression is to use De Morgan's theorem.
• It is highly recommended to place parentheses around terms where lines have been broken.

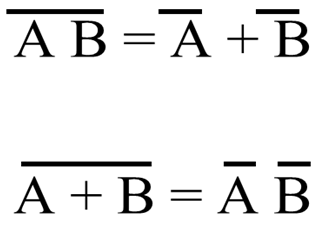
For example:

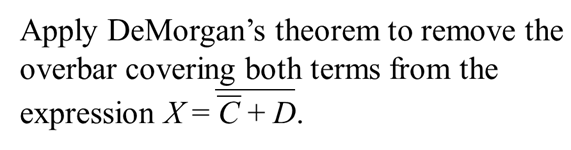
DeMorgan (cont.)

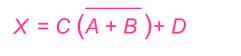
Applying DeMorgan's theorem and the distribution law:

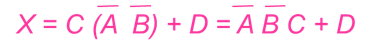
Bubble Pushing

• Bubble pushing is a technique to apply De Morgan's theorem directly to the logic diagram.
1. Change the logic gate (AND to OR and OR to AND).
2. Add bubbles to the inputs and outputs where there were none, and remove the original bubbles.
• Logic gates can be De Morganized so that bubbles appear on inputs or outputs in order to satisfy signal conditions rather than specific logic functions. An active-low signal should be connected to a bubble on the input of a logic gate.

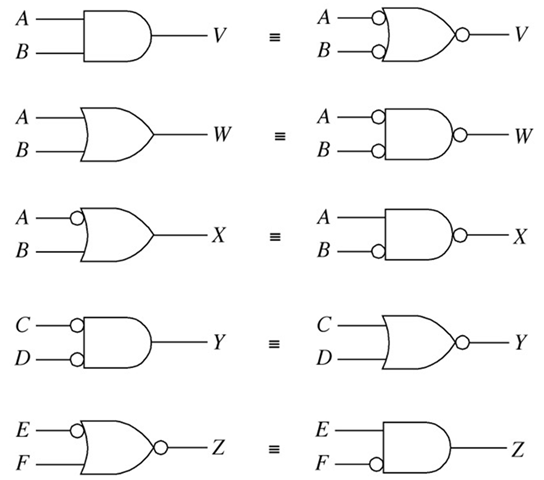
The Universal Capability of NAND and NOR Gates

• NAND and NOR gates are universal logic gates.
• The AND, Or, Nor and Inverter functions can all be performed using only NAND gates.
• The AND, OR, NAND and Inverter functions can all be performed using only NOR gates.
• An inverter can be made from a NAND or a NOR by connecting all inputs of the gate together.
• If the output of a NAND gate is inverted, it becomes an AND function.
• If the output of a NOR gate is inverted, it becomes an OR function.
• If the inputs to a NAND gate are inverted, the gate becomes an OR function.
• If the inputs to a NOR gate are inverted, the gate becomes an AND function.
• When NAND gates are used to make the OR function and the output is inverted, the function becomes NOR.
• When NOR gates are used to jake the AND function and the output is inverted, the function becomes NAND.

AND-OR-Invert Gates for Implementing Sum-of-Products Expressions

• Most Boolean reductions result in a Product-of-Sums (POS) expression or a Sum-of-Products (SOP) expression.
• The Sum-of-Products means the variables are ANDed to form a term and the terms are ORed. X = AB + CD.
• The Product-of-Sums means the variables are ORed to form a term and the terms are ANDed. X = (A + B)(C + D)
• AND-OR-Inverter gate combinations (AOI) are available in standard ICs and can be used to implement SOP expressions.
• The 74LS54 is a commonly used AOI.
• Programmable Logic Devices (PLDs) are available for larger and more complex functions than can be accomplished with an AOI.

Karnaugh Mapping

• Karnaugh mapping is a graphic technique for reducing a Sum-of-Products (SOP) expression to its minimum form.
• Two, three and four variable k-maps will have 4, 8 and 16 cells respectively.
• Each cell of the k-map corresponds to a particular combination of the input variable and between adjacent cells only one variable is allowed to change.
• Use the following steps to reduce an expression using a k-map.
1. Use the rules of Boolean Algebra to change the expression to a SOP expression.
2. Mark each term of the SOP expression in the correct cell of the k-map. (kind of like the game Battleship)
3. Circle adjacent cells in groups of 2, 4 or 8 making the circles as large as possible. (NO DIAGONALS!)
4. Write a term for each circle in a final SOP expression. The variables in a term are the ones that remain constant across a circle.
• The cells of a k-map are continuous left-to-right and top-to-bottom. The wraparound feature can be used to draw the circles as large as possible.
• When a variable does not appear in the original equation, the equation must be plotted so that all combinations of the missing variable(s) are covered.

 This is a very visual problem so watch the video for examples on how to complete and solve Karnaugh Maps!

Additional Notes

In some cases the question arises as to the order of operations. If an AND and an OR appear in the same expression, which is to be done first? The order of operations of Boolean Algebra are the same as standard algebra. The AND operation (same as multiplication) is performed first. Of course, parentheses can be used to alter the order of operations just as in standard algebra. In the expression AB + C, A is ANDed to B then ORed with C. In the expression, A(B + C), B is ORed with C first, then ANDed with A.

A function inside a parentheses must be accomplished first before any functions outside the parentheses. A bar over several variables can also act as a parentheses. Any function under the bar must be done before any functions not under the bar.