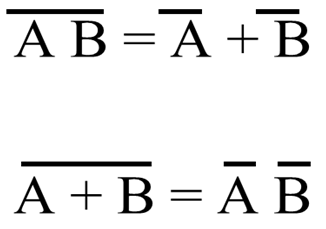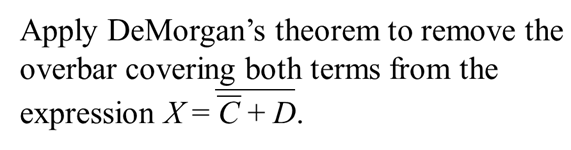DeMorgan's Theorem

De Morgan's theorem allows large bars in a Boolean Expression to be broken up into smaller bars over individual variables.
De Morgan's theorem says that a large bar over several variables can be broken between the variables if the sign between the variables is changed.
De Morgan's theorem can be used to prove that a NAND gate is equal to an OR gate with inverted inputs.
De Morgan's theorem can be used to prove that a NOR gate is equal to an AND gate with inverted inputs.
In order to reduce expressions with large bars, the bars must first be broken up. This means that in some cases, the first step in reducing an expression is to use De Morgan's theorem.
It is highly recommended to place parentheses around terms where lines have been broken.

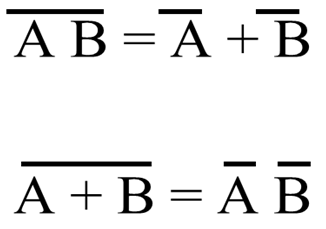
For example: