Combinational Logic

Several of the basic logic gates are used to form a more complex function with combinational logic. A Boolean equation can be used to describe any combinational logic circuit. The Boolean equation is written in a form that will satisfy the problem.

 

We have seen how to express single gate expressions like X=A+B for an OR gate and F=D*G for the AND gate. Now we will look at combinational logic and Boolean expressions.

Converting a logic diagram to a Boolean expression

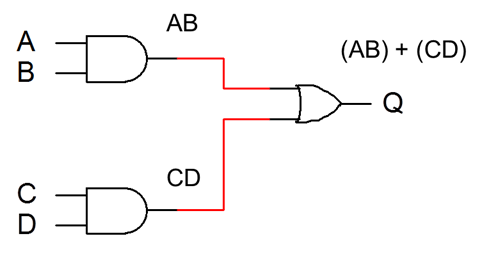
Given the logic gates below. First look at how the gates are connected to each other. Notice how there are 2 sets of AND gates going into an OR gate. Lay it out logically like this (something AND something) OR (something AND something).

In this case it would be: (A AND B) OR (C AND B) Change the AND / OR to their Boolean symbols and you have: (A*B) + (C*D). So Q=(AB) + (CD)  (Notice The AND gates are generally grouped together with parenthesis. I also dropped the *. When terms are placed next to one another a multiplication is implied.

 

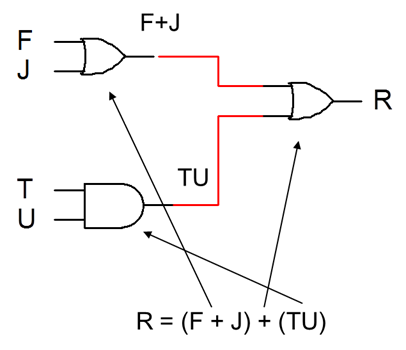
Here is another example

• Keeping gates together, think about how they are grouped.
• F and J are going into an OR gate.
• T and U are going into an AND gate
• The outputs of those 2 gates goes to an OR gate.
• The final output would be: R = (F + J) + (TU)

 

 

 

---

 

When NAND and NOR gates are used. Just make sure you place the bar over the expression that is inverted.

 

 

 

return to top | previous page | next page